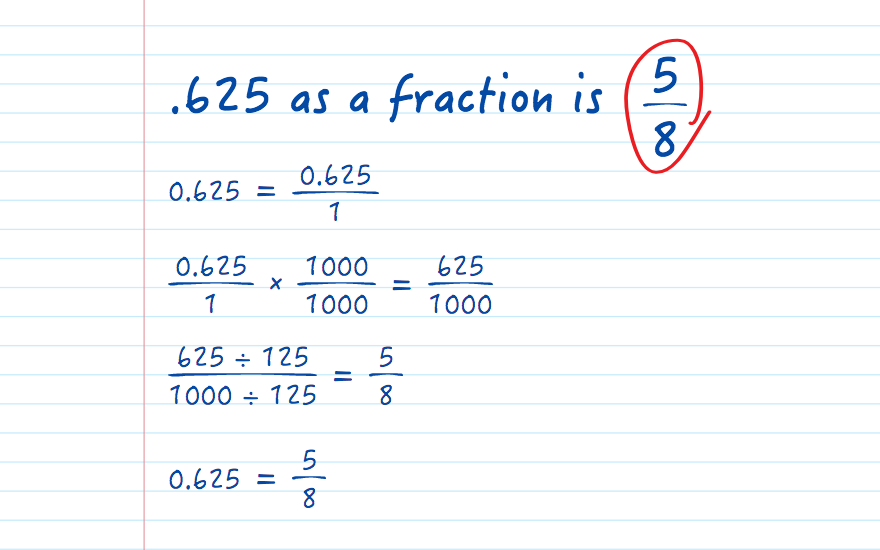Are you struggling to convert .625 into a fraction? You’re not alone! Many people find themselves puzzled when it comes to understanding decimals as fractions. In this article, we will explore the concept of .625 as a fraction, breaking it down step by step to make it easier for you to grasp.
Decimals and fractions are two fundamental aspects of mathematics that we encounter daily, whether in school, at work, or even in everyday life. Knowing how to convert decimals like .625 into fractions is essential for solving various mathematical problems and real-world applications.
This article aims to provide a detailed explanation of .625 as a fraction, including its conversion process, practical applications, and tips for mastering this concept. By the end, you’ll have a solid understanding of this topic and be able to apply it confidently.
Read also:Muni Long Family An Indepth Exploration Of Their Musical Dynasty
Table of Contents
- What is .625 as a Fraction?
- Converting Decimals to Fractions
- Step-by-Step Process of Converting .625
- Common Fractions and Their Decimal Equivalents
- Practical Applications of Fractions
- Simplifying Fractions
- Tips for Mastering Fractions
- Frequently Asked Questions
- Resources for Learning More About Fractions
- Conclusion
What is .625 as a Fraction?
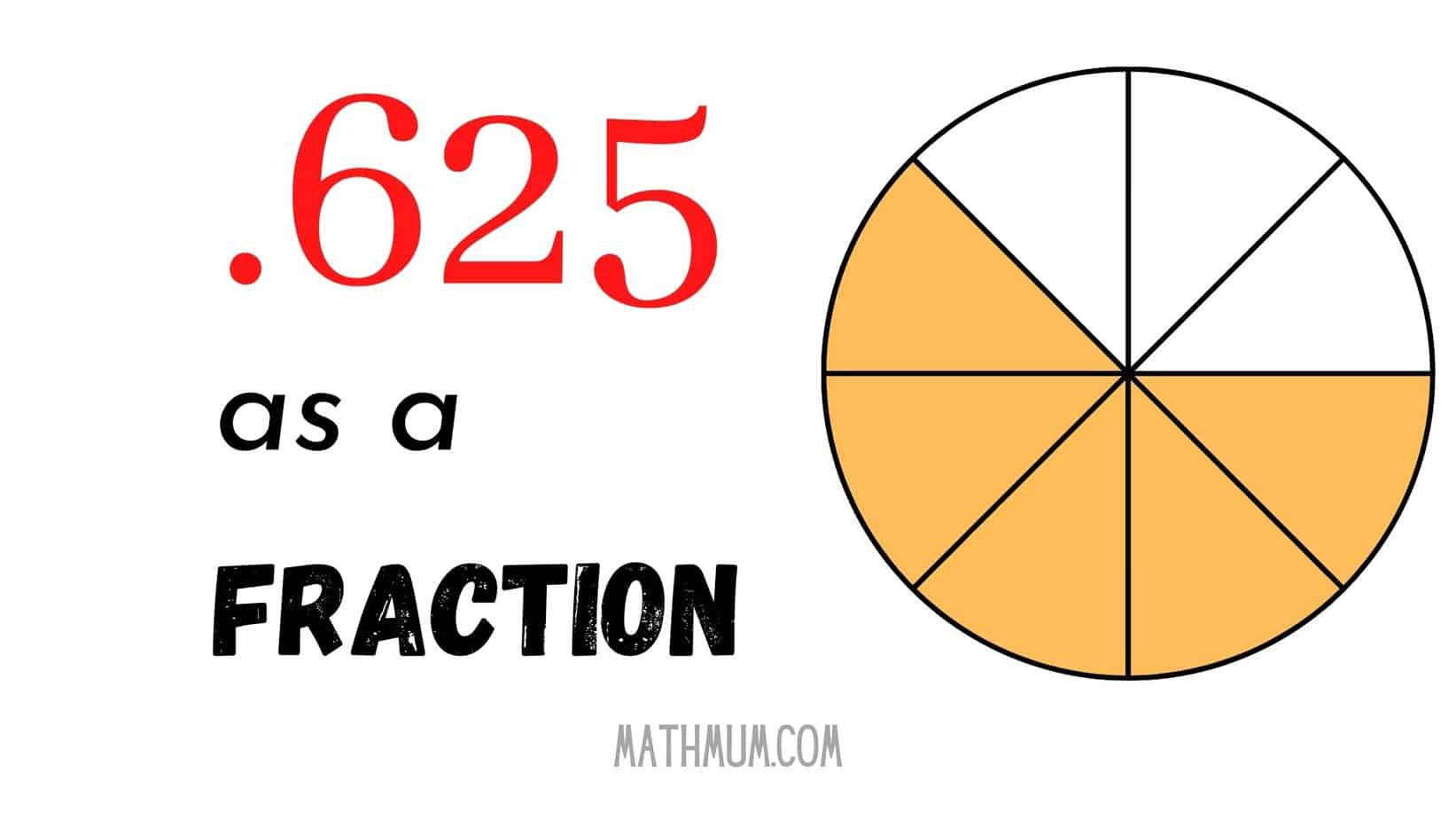
When we talk about .625 as a fraction, we are essentially converting a decimal into its fractional equivalent. In mathematical terms, .625 can be expressed as 5/8. This means that .625 is equal to five-eighths.
Why is .625 Important?
.625 is significant because it is a commonly encountered decimal in various fields, such as engineering, construction, and finance. Understanding how to convert .625 into a fraction allows you to perform calculations more accurately and efficiently.
Converting Decimals to Fractions
The process of converting decimals to fractions involves understanding the place value of the decimal and simplifying the resulting fraction. Let’s take a closer look at how this works:
Understanding Decimal Place Values
- Decimals represent parts of a whole number.
- Each digit in a decimal has a specific place value, such as tenths, hundredths, or thousandths.
- For example, in .625, the digit 6 is in the tenths place, 2 is in the hundredths place, and 5 is in the thousandths place.
Step-by-Step Process of Converting .625
Converting .625 into a fraction involves the following steps:
- Write down the decimal as a fraction with 1 as the denominator: .625/1.
- Multiply both the numerator and denominator by 1000 to eliminate the decimal point: (625/1000).
- Simplify the fraction by finding the greatest common divisor (GCD) of 625 and 1000. The GCD of 625 and 1000 is 125.
- Divide both the numerator and denominator by the GCD: (625 ÷ 125)/(1000 ÷ 125) = 5/8.
Common Fractions and Their Decimal Equivalents
Understanding common fractions and their decimal equivalents can help you quickly convert decimals to fractions. Below is a table of commonly used fractions:
| Fraction | Decimal Equivalent |
|---|---|
| 1/2 | 0.5 |
| 1/4 | 0.25 |
| 3/4 | 0.75 |
| 1/8 | 0.125 |
| 5/8 | 0.625 |
Practical Applications of Fractions
Fractions are used in various real-world scenarios. Here are some examples:
Read also:Diddy Height And Weight The Inside Story Of A Hiphop Legend
In Cooking
Chefs and home cooks often use fractions to measure ingredients accurately. For instance, a recipe might call for 3/4 cup of sugar or 1/2 teaspoon of salt.
In Construction
Builders and engineers rely on fractions to ensure precise measurements. For example, a wall might need to be 5/8 inch thick to meet building codes.
In Finance
Fractions are also used in finance, particularly when calculating interest rates or dividing assets. For instance, an investor might own 3/8 of a company’s shares.
Simplifying Fractions
Simplifying fractions involves reducing them to their lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). This process makes fractions easier to work with and understand.
How to Simplify Fractions
- Find the GCD of the numerator and denominator.
- Divide both the numerator and denominator by the GCD.
- Write the simplified fraction.
Tips for Mastering Fractions
Mastering fractions requires practice and a solid understanding of basic mathematical concepts. Here are some tips to help you improve your skills:
Practice Regularly
Set aside time each day to practice converting decimals to fractions and simplifying fractions. The more you practice, the more comfortable you’ll become with the process.
Use Visual Aids
Visual aids, such as fraction circles or number lines, can help you visualize fractions and understand their relationships.
Learn from Mistakes
Don’t be discouraged by mistakes. Instead, use them as learning opportunities to improve your understanding of fractions.
Frequently Asked Questions
Here are some common questions about .625 as a fraction:
Q1: Is .625 a terminating decimal?
Yes, .625 is a terminating decimal because it has a finite number of digits after the decimal point.
Q2: Can .625 be expressed as a mixed number?
No, .625 cannot be expressed as a mixed number because it is less than 1. However, it can be expressed as a proper fraction: 5/8.
Q3: What is the reciprocal of .625?
The reciprocal of .625 is 1.6, which can be expressed as the fraction 8/5.
Resources for Learning More About Fractions
If you want to learn more about fractions, here are some resources to consider:
- Khan Academy: Offers free lessons on fractions and other mathematical concepts.
- Math Is Fun: Provides interactive tools and explanations for learning fractions.
- Mathway: A useful tool for solving fraction-related problems.
Conclusion
In conclusion, understanding .625 as a fraction is a valuable skill that can be applied in various fields. By following the step-by-step process outlined in this article, you can easily convert decimals like .625 into fractions and simplify them as needed.
We encourage you to practice regularly and explore the resources mentioned above to deepen your understanding of fractions. If you found this article helpful, please share it with others and leave a comment below. Your feedback is valuable to us!